算法篇之排序

发表于 更新于 分类于

初衷

为什么我要写算法篇，记得刚入大学的第一节课，老师就教我们软件=算法+数据结构，而我恰恰这两点学的最差了，学习这块两个初衷：1.阿里机试折腰，让我清楚的意识到自己的问题 2.职业瓶颈，已经工作四年了，知识面有了，但是缺乏深度。暂且先选择将基础算法打扎实点。

声明以下所有的定义不具有权威性，皆来自我对该算法的理解。

1.初级排序

1.1冒泡法

这大概是最简答的排序，可我一直是搞错的。
定义：将数组相邻的数进行对比，直到选出最大值或者最小值，每次冒出一个数，后面的逻辑不再处理它
实现：

1
2
3
4
5
6
7
8
9
10
11
// 从小到大排序
for (int i = 0; i < wait2Sort.length-1; i++) {// 控制循环次数
	for (int j = 0; j < wait2Sort.length - 1 - i; j++) {
		if (wait2Sort[j] > wait2Sort[j + 1]) {
			int temp = wait2Sort[j];
			wait2Sort[j] = wait2Sort[j + 1];
			wait2Sort[j + 1] = temp;
		}

	}
}

N个数字要排序完成，总共进行N-1趟排序，每第 i 趟的排序次数为 (N-i) 次，所以可以用双重循环语句，外层控制循环多少趟，内层控制每一趟的循环次数。

按说算法是这样的确实没错，但是网络上还有另外一种写法，就是第一层循环N次，按说是结果不会错，但是算法多此一举。我想追究的是会不会多算一次。例如如下写法：

1
2
3
4
5
6
7
8
9
10
11
// 从小到大排序
for (int i = 0; i < wait2Sort.length; i++) {// 控制循环次数
	for (int j = 0; j < wait2Sort.length - 1 - i; j++) {
		if (wait2Sort[j] > wait2Sort[j + 1]) {
			int temp = wait2Sort[j];
			wait2Sort[j] = wait2Sort[j + 1];
			wait2Sort[j + 1] = temp;
		}

	}
}

至于N次是否进行运算，我们就需要探讨当i=N-1时，是否进入第二个循环，当i=N-1时，第二个循环的条件就变成了j<N-1-(N-1)即j<0，这个永远不会成立，因此最后一次的循环不会进入二层循环。相对于正确算法只多了一次判断，性能可以忽略不计。

1.2选择排序法

1.2.1初阶选择排序法

定义：选取确定的数据依次与其他数据进行对比
实现：

1
2
3
4
5
6
7
8
9
10
// 从小到大排序
for (int i = 0; i < wait2Sort.length - 1; i++) {
	for (int j = i + 1; j < wait2Sort.length; j++) {
		if (wait2Sort[i] > wait2Sort[j]) {
			int temp = wait2Sort[j];
			wait2Sort[j] = wait2Sort[i];
			wait2Sort[i] = temp;
		}
	}
}

1.2.2进阶选择排序法

定义：选取确定的数据依次与其他数据进行对比，但是和1.2.1区别在于内部循环只确定最大数的索引，数据交换是在外层循环做的。
实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 从小到大排序
for (int i = 0; i < wait2Sort.length-1; i++) {
	int min = i;
	for (int j = i + 1; j < wait2Sort.length; j++) {
		if (wait2Sort[min] > wait2Sort[j]) {
			min = j;
		}
	}

	if (min != i) {
		int temp = wait2Sort[min];
		wait2Sort[min] = wait2Sort[i];
		wait2Sort[i] = temp;
	}
}

该算法较1.2.1区别在于内部循环只确定最大数的索引，数据交换是在外层循环做的。少了多次交换，相较于前两种性能更好！

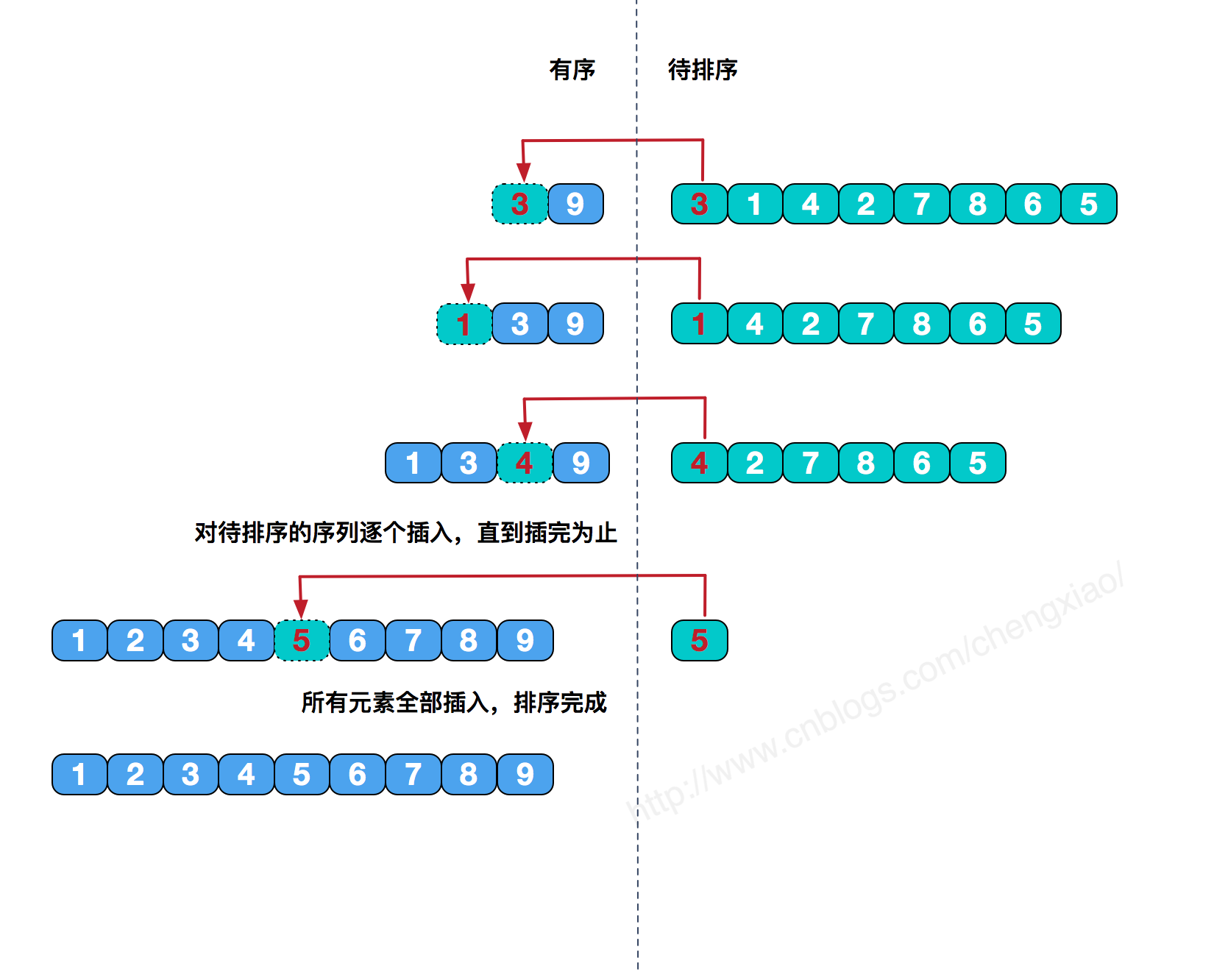
1.3插入排序

定义：像整理牌一样，将每一张牌插入到有序数组中适当的位置。左侧永远是有序的，当运行到数据最右端，即排序完毕，这种算法对于数组中部分数据是有序的话，性能会有很大的提升！
实现：

1
2
3
4
5
6
7
8
// 从小到大排序
for (int i = 1; i < wait2Sort.length; i++) {
	for (int j = i; j > 0 && (wait2Sort[j - 1]) > wait2Sort[j]; j--) {
		int temp = wait2Sort[j];
		wait2Sort[j] = wait2Sort[j - 1];
		wait2Sort[j - 1] = temp;
	}
}

1.4希尔排序

定义：希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止
实现:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 从小到大排序
int h = 1;
while (h < wait2Sort.length / 3)
	h = 3 * h + 1;
while (h >= 1) {
	for (int i = h; i < wait2Sort.length; i++) {
		for (int j = i; j - h >= 0 && wait2Sort[j - h] > wait2Sort[j]; j = j - h) {
			int temp = wait2Sort[j - h];
			wait2Sort[j - h] = wait2Sort[j];
			wait2Sort[j] = temp;
		}
	}

	h = h / 3;
}

上面已经演示了以4为初始间隔对包含10个数据项的数组进行排序的情况。对于更大的数组开始的间隔也应该更大。然后间隔不断减小，直到间隔变成1。

举例来说，含有1000个数据项的数组可能先以364为增量，然后以121为增量，以40为增量，以13为增量，以4为增量，最后以 1为增量进行希尔排序。用来形成间隔的数列被称为间隔序列。这里所表示的间隔序列由Knuth提出，此序列是很常用的。在排序算法中，首先在一个短小的循环中使用序列的生成公式来计算出最初的间隔。h值最初被赋为1，然后应用公式h=3*h+1生成序列1,4,13,40,121,364，等等。当间隔大于数组大小的时候，这个过程停止。

1
2
3
4
5
6
7
8
9
10
11
// 从小到大排序
for (int h = wait2Sort.length / 2; h > 0; h = h / 2) {
	for (int i = h; i < wait2Sort.length; i++) {
		for (int j = i; j>=h && wait2Sort[j - h] > wait2Sort[j]; j = j - h) {
			int temp = wait2Sort[j];
			wait2Sort[j] = wait2Sort[j - h];
			wait2Sort[j - h] = temp;
		}
	}

}

这个也是正确的，间距为N/2

2.归并排序

定义：归并排序,也叫归并算法，指的是将两个顺序序列合并成一个顺序序列的方法

如　设有数列{6，202，100，301，38，8，1}
初始状态：6,202,100,301,38,8,1
第一次归并后：{6,202},{100,301},{8,38},{1}，比较次数：3；
第二次归并后：{6,100,202,301}，{1,8,38}，比较次数：4；
第三次归并后：{1,6,8,38,100,202,301},比较次数：4；
总的比较次数为：3+4+4=11；
逆序数为14；

实现:

3.快速排序

4.堆排序

总结

参考

  1. 图解排序算法(二)之希尔排序